88. Merge Sorted Array

Problem

ou are given two integer arrays nums1 and nums2, sorted in non-decreasing order, and two integers m and n, representing the number of elements in nums1 and nums2 respectively.

Merge nums1 and nums2 into a single array sorted in non-decreasing order.

The final sorted array should not be returned by the function, but instead be stored inside the array nums1. To accommodate this, nums1 has a length of m + n, where the first m elements denote the elements that should be merged, and the last n elements are set to 0 and should be ignored. nums2 has a length of n.

Example 1:

Input: nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 Output: [1,2,2,3,5,6] Explanation: The arrays we are merging are [1,2,3] and [2,5,6]. The result of the merge is [1,2,2,3,5,6] with the underlined elements coming from nums1.

Example 2:

Input: nums1 = [1], m = 1, nums2 = [], n = 0 Output: [1] Explanation: The arrays we are merging are [1] and []. The result of the merge is [1].

Example 3:

Input: nums1 = [0], m = 0, nums2 = [1], n = 1 Output: [1] Explanation: The arrays we are merging are [] and [1]. The result of the merge is [1]. Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.

Constraints:

  • nums1.length == m + n

  • nums2.length == n

  • 0 <= m, n <= 200

  • 1 <= m + n <= 200

  • -109 <= nums1[i], nums2[j] <= 109

Follow up: Can you come up with an algorithm that runs in O(m + n) time?

Solution

Approach 1: Merge and sort

Intuition

A naive approach would be to simply write the values from nums2 into the end of nums1, and then sort nums1. Remember that we do not need to return a value, as we should modify nums1 in-place. While straightforward to code, this approach has a high time complexity as we're not taking advantage of the existing sorting.

Implementation

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        # Write the elements of num2 into the end of nums1.
        for i in range(n):
            nums1[i + m] = nums2[i]

  • Time complexity: O((n+m)log⁡(n+m))\mathcal{O}((n + m)\log(n + m))O((n+m)log(n+m)).

    The cost of sorting a list of length xxx using a built-in sorting algorithm is O(xlog⁡x)\mathcal{O}(x \log x)O(xlogx). Because in this case, we're sorting a list of length m+nm + nm+n, we get a total time complexity of O((n+m)log⁡(n+m))\mathcal{O}((n + m) \log (n + m))O((n+m)log(n+m)).

  • Space complexity: O(n)\mathcal{O}(n)O(n), but it can vary.

    Most programming languages have a built-in sorting algorithm that uses O(n)\mathcal{O}(n)O(n) space.

Approach 2: Three Pointers (Start From the Beginning)

Intuition

Because each array is already sorted, we can achieve an O(n+m)\mathcal{O}(n + m)O(n+m) time complexity with the help of the two-pointer technique.

Algorithm

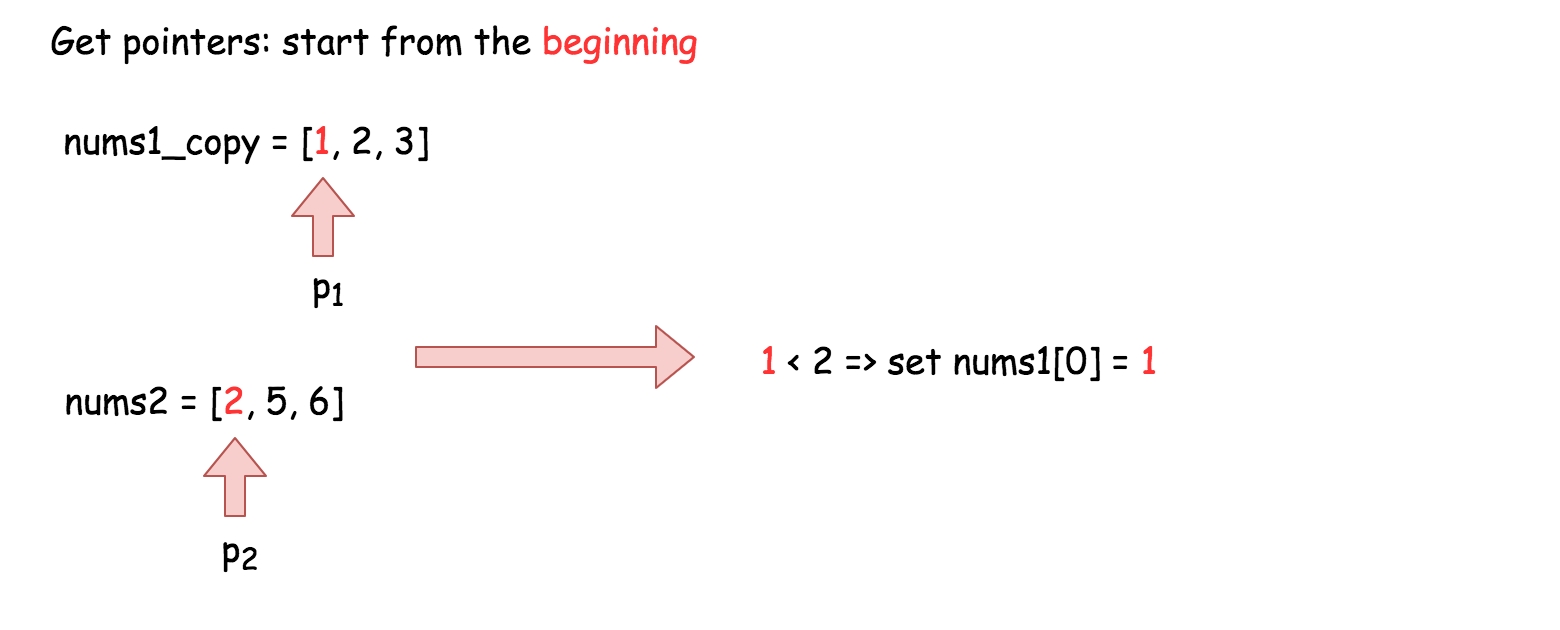
The simplest implementation would be to make a copy of the values in nums1, called nums1Copy, and then use two read pointers and one write pointer to read values from nums1Copy and nums2 and write them into nums1.

  • Initialize nums1Copy to a new array containing the first m values of nums1.

  • Initialize the read pointer p1 to the beginning of nums1Copy.

  • Initialize the read pointer p2 to the beginning of nums2.

  • Initialize the write pointer p to the beginning of nums1.

  • While p is still within nums1:

    • If nums1Copy[p1] exists and is less than or equal to nums2[p2]:

      • Write nums1Copy[p1] into nums1[p], and increment p1 by 1.

    • Else

      • Write nums2[p2] into nums1[p], and increment p2 by 1.

    • Increment p by 1.

compute

Implementation

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        # Make a copy of the first m elements of nums1.
        nums1_copy = nums1[:m]

        # Read pointers for nums1Copy and nums2 respectively.
        p1 = 0
        p2 = 0

        # Compare elements from nums1Copy and nums2 and write the smallest to nums1.
        for p in range(n + m):
            # We also need to ensure that p1 and p2 aren't over the boundaries
            # of their respective arrays.
            if p2 >= n or (p1 < m and nums1_copy[p1] <= nums2[p2]):
                nums1[p] = nums1_copy[p1]
                p1 += 1
            else:
                nums1[p] = nums2[p2]
                p2 += 1

Complexity Analysis

  • Time complexity: O(n+m)\mathcal{O}(n + m)O(n+m).

    We are performing n+2⋅mn + 2 \cdot mn+2⋅m reads and n+2⋅mn + 2 \cdot mn+2⋅m writes. Because constants are ignored in Big O notation, this gives us a time complexity of O(n+m)\mathcal{O}(n + m)O(n+m).

  • Space complexity: O(m)\mathcal{O}(m)O(m).

    We are allocating an additional array of length mmm.

Approach 3: Three Pointers (Start From the End)

Intuition

Interview Tip: This is a medium-level solution to an easy-level problem. Many of LeetCode's easy-level problems have more difficult solutions, and good candidates are expected to find them.

Approach 2 already demonstrates the best possible time complexity, O(n+m)\mathcal{O}(n + m)O(n+m), but still uses additional space. This is because the elements of array nums1 have to be stored somewhere so that they aren't overwritten.

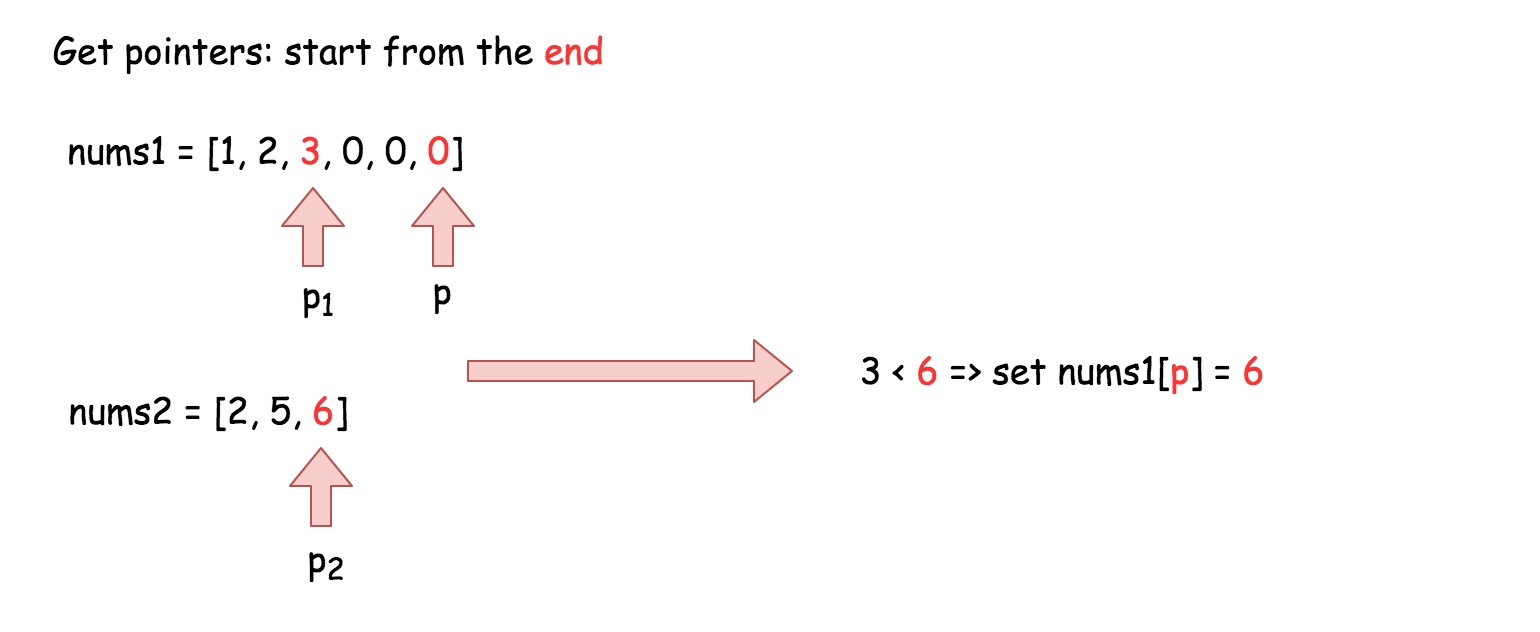
So, what if instead we start to overwrite nums1 from the end, where there is no information yet?

The algorithm is similar to before, except this time we set p1 to point at index m - 1 of nums1, p2 to point at index n - 1 of nums2, and p to point at index m + n - 1 of nums1. This way, it is guaranteed that once we start overwriting the first m values in nums1, we will have already written each into its new position. In this way, we can eliminate the additional space.

Interview Tip: Whenever you're trying to solve an array problem in place, always consider the possibility of iterating backwards instead of forwards through the array. It can completely change the problem, and make it a lot easier.

compute

Implementation

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """

        # Set p1 and p2 to point to the end of their respective arrays.
        p1 = m - 1
        p2 = n - 1

        # And move p backward through the array, each time writing
        # the smallest value pointed at by p1 or p2.
        for p in range(n + m - 1, -1, -1):
            if p2 < 0:
                break
            if p1 >= 0 and nums1[p1] > nums2[p2]:
                nums1[p] = nums1[p1]
                p1 -= 1
            else:
                nums1[p] = nums2[p2]
                p2 -= 1
Current

1 / 6

Complexity Analysis

  • Time complexity: O(n+m)\mathcal{O}(n + m)O(n+m).

    Same as Approach 2.

  • Space complexity: O(1)\mathcal{O}(1)O(1).

    Unlike Approach 2, we're not using an extra array.

Proof (optional)

You might be a bit skeptical of this claim. Does it really work in every case? Is it safe to be making such a bold claim?

This way, it is guaranteed that once we start overwriting the first m values in nums1, we will have already written each into its new position. In this way, we can eliminate the additional space.

Great question! So, why does this work? To prove it, we need to ensure that p never overwrites a value in nums1 that p1 hasn't yet read from nums1.

Words of Advice: Terrified of proofs? Many software engineers are. Good proofs are simply a series of logical assertions, each building on the next. In this way, we can go from "obvious" statements, all the way to the one we want to prove. I recommend reading each statement one by one, ensuring that you understand each before moving to the next.

  1. We know that upon initialization, p is n steps ahead of p1 (in other words, p1 + n = p).

  2. We also know that during each of the p iterations this algorithm performs, p is always decremented by 1, and either p1 or p2 is decremented by 1.

  3. We can deduce that when p1 decremented, the gap between p and p1 stays the same, so there can't be an "overtake" in that case.

  4. We can also deduce that when p2 is decremented though, the gap between p and p1 shrinks by 1 as p moves, but not p1.

  5. And from that, we can deduce that the maximum number of times that p2 can be decremented is n. In other words, the gap between p and p1 can shrink by 1, at most n times.

  6. In conclusion, it's impossible for an overtake to occur, as they started n apart. And when p = p1, the gap has to have shrunk n times. This means that all of nums2 have been merged in, so there is nothing more to do.

PreviousproblemsNextLearning

Last updated